Incorrect header width for scrollable table in IE11
Incorrect header width for scrollable table in IE11
Hi,
After migrating from version 1.10.25 to version 1.11.3 I’m observing problems with column header width in Internet Explorer 11.
The related table are created using ‘scrollY: 200’. As result table header and body are two different tables in DOM and datatables provides some calculations to make header table and body table columns width equal.
But, after the migration I can see next:
Expected result
Header table columns and body table columns width should be equal.
Actual result
Corresponding columns from header and body table might have different width

Currently, it hard to me to reproduce it outside my environment but it seems that the issue depends on cell contents. For me it reproduced for some columns with icons or checkboxes(Perhaps it depends on inner content size, padding or other attributes).
By looking on datatables changes I would say that the current situations is triggered by next changes:

As we can see:
In version 1.10.25:
Column width has been calculated using **‘$(nSizer).css('width')’ **expression
In version 1.11.3
Column width is calculated using
‘window.getComputedStyle(nSizer).width’ expression if window.getComputedStyle is supported by browser or
using ‘$(nSizer).width()’ expression in other case.
Second expression is used for my case as window.getComputedStyle doesn’t implemented for IE11.
And from what I can see that the second ‘$(nSizer).width()’ might give different result than window.getComputedStyle method.
I’ve tried to debug results from old and two new expressions, and I see next results for my example for the column with width 39px:
1. Old expression ‘$(nSizer).css('width')’ gives 39px
2. window.getComputedStyle also gives 39px
3. But for ‘$(nSizer).width()’ gives 13px which isn’t correct value.
After that incorrect value is assigned to body table header:
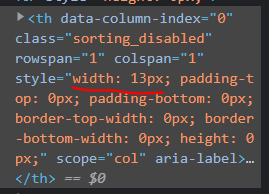
And then it looks like header table use this incorrect value to adjust its width and it gives us the resulted behavior with different column size described above.
So, it looks that problem is in using ‘$(nSizer).width()’ expression which could return different result than window.getComputedStyle.
Hence this situation could affect any browser where window.getComputedStyle isn’t implemented.
So, for me it looks that width() method isn’t reliable enough her to use it for column width calculation.
Can we consider this situation as a regression bug?
Could this situation be fixed by using ‘$(nSizer).css('width')’ expression instead of the ‘$(nSizer).width()’ to return previous cross-browser behavior?
Cause, as I observe in my case ‘$(nSizer).css('width')’ and window.getComputedStyle always gives the same result but ‘$(nSizer).width()’ according to cell content might returns different result.
Or, perhaps you could suggest alternative solution.
Best Regards
Answers
Thanks for flagging this up.
getCompletedStyleis available in IE11. Are you getting errors in IE11 saying it isn't? Might you be using the browser in quirks or compatibility mode?Allan
Thanks for the answer Allan. Yes, you are right. Thanks for this catch. getCompletedStyle is implemented in IE11as you say. I wrongly described my test case with methods behavior for Chrome instead of IE11.
The
getCompletedStyleis implemented but anyway returns incorrect width.Here is correct exmple with all 3 methods in IE11 for the column that have actual width 539px:
1. Old expression
$(nSizer).css('width')gives 539px (Version 1.10.25)2.
window.getComputedStylegives 501.5px (Version 1.11.3)3.
$(nSizer).width()gives 502px (Version 1.11.3)Hence it looks that both new methods might return width different that it was in version 1.10.25. So the problem is in
getComputedStylemethod that returns unexpected width for IE11. And this seems to be the real cause of the described behavior.I've just tried this example in IE11 and it appears to be working okay. Does it for you? If not, can you give me a link to a page which is showing the is issue for you?
I would expect getComputedStyle to be smaller and css('width'), depending on the box model of the table cells.
Allan
Allan, your example works correct.
But my case is more specyfic. I've prepared simplified example wher the issue is reproduced:
Here is index.html
Here is main.js
And here is main.css
And this example using datatables 1.11.3 looks next in IE11:

But if change version to 1.10.25 it will look next:

It seems that problems comes from combination of using
box-sizing: border-box;on th element and fixed size of columns added in table configuration.Removing
box-sizing: border-box;from th element makes table looks correct.But, anyway version 1.10.25 doesn't have problem with this attribute but 1.11.3 does.
Seems previously used approach for columns widht calculation looks more reliable for the described case.
Could you give me a link to a test case showing the issue please? For example I don't know what is in your main.css and main.js. If our example is working correctly, then something on the page must be interacting with the table, which is why I'll need a test case to be able to take this any further.
Allan
Hi , Allan
I've include all required CSS and JS code to index.html file for convinience.
See the complete index.html for this case below:
Just copy this content and create your own index.html. Then use the next test case:
1) Open the attached index.html using IE11

Expected result:
Columns and headers size should be equal.
Actual result:
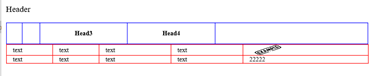
Column size is broken
2) Edit the attached index.html and change datatables version from 1.11.3 to 1.10.25

3) Open the attached index.html using IE11
Actual result 2:
Column size is ok
Could you create a test case that demonstrates the issue on http://live.datatables.net/ or jsfiddle please, seeing the problem would help us support you more effectively.
Colin
Colin, sure
Here is a live example:
http://live.datatables.net/pocuqeta/1/edit
Thanks for the test case, but it's giving a syntax error on line 1. Please can you take a look and ensure it demonstrates the issue you want help with.
Colin
Oh, missed it. Here is example without syntax error:
http://live.datatables.net/hibusixe/1/edit
Regards,
Volodymyr
It's still not running: "Uncaught SyntaxError: Unexpected token '<'"
Colin
Sorry, missed old <script> tag.
Next example should be good:
http://live.datatables.net/fupitege/1/edit
And 'Run with JS should' be clicked to reproduce the issue.
Thanks for fixing that. It's the empty columns that's causing the issues. I found there are two ways to address it,
columns: this.columnsto becolumnDefs: this.columns,this.columns.push(null);Colin
Hi Colin, thanks for your suggestions.
I’ve tried what you recommend but still have issues.
1) About ‘Change columns: this.columns to be columnDefs: this.columns’
If I do this this will be incorrect configuration as columnDefs expects array with objects like
{ targets: [0], width: ‘30px’}while here we have objects like{ width: ‘30px’}.So, I’ve changed the example to have correct configuration, but problems persist. See updated example:
http://live.datatables.net/canuleso/3/edit
2) About ‘Remove the two this.columns.push(null);’
By do this I’ll also get incorrect configuration as documentation says next:
https://datatables.net/reference/option/columns
So, by doing this I’ll have another getting "
Script error. (line 0)"I still suppose that problems come from
getCompletedStylemethod which was introduced in 1.11.3.Looks this method isn’t full reliable to calculate column width in IE11. Previously used ``$(nSizer).css('width')
works more stable in IE11 thanwindow.getComputedStyle(nSizer).widthI’m able to locally fix this case included to datatables code a fragment which checks browser type and use old method to calculate columns width if browser is IE. This returns an old behavior.
But as we need to use an official version it is not an option.
Perhaps, similar fix could be included in datatables if it is acceptable?
Cause the new method looks problematic for IE11. Potentially it could cause another similar issue related to columns width for some another cases.
Thanks in advance,
Volodymyr
This is with the two lines commented out - http://live.datatables.net/fupitege/7/edit . The table is loading as expected for me in IE11. Is that not the case for you?
Colin
Colin,
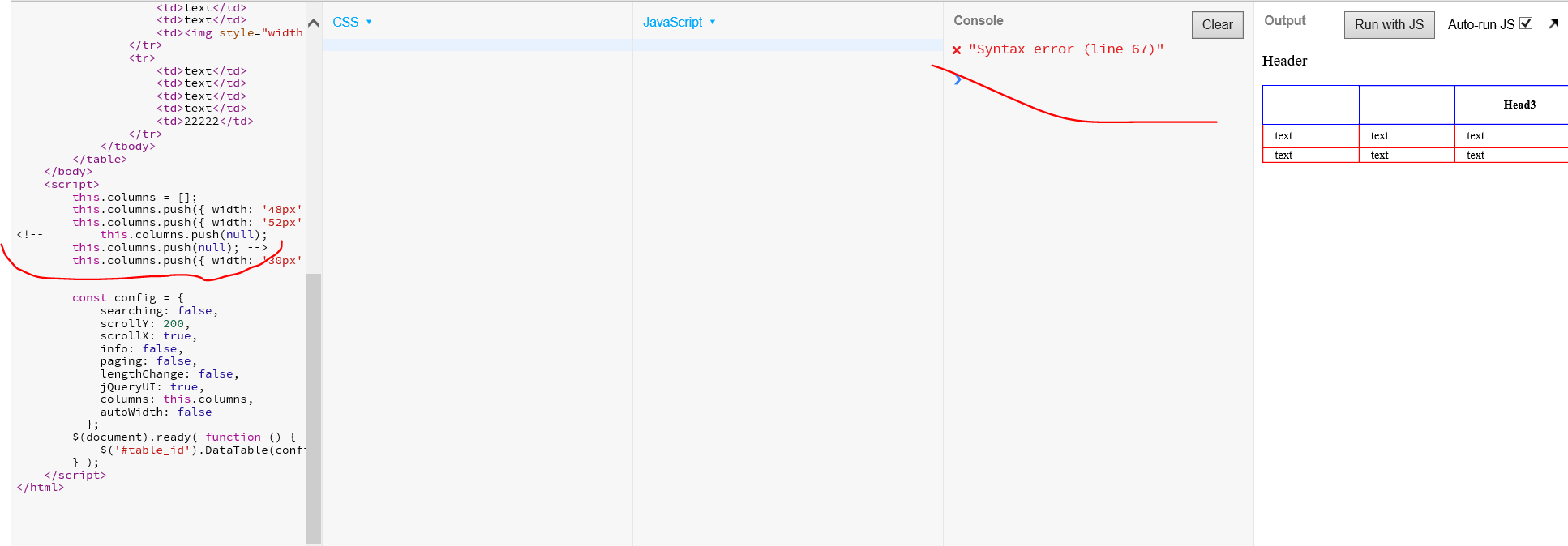
Still having an error with your example and table width is default.
Same problem as described in my previous comment.
Volodymyr
Sorry, I apologise, I entirely missed that. I took a better look, and it appears the CSS is missing. Taking your test case under 1 above, I added the CSS file in and it's behaving as expected now in IE11 - see here. I guess the more modern browsers have different defaults that just mean it works.
Can you take a look, please, and see if that's working for you.
Colin
Hi Colin,
Thanks for a new example.
I’ve checked it but still there are some problem.
1) Problem is still persisting after resizing
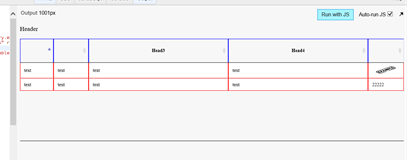
After the example is opened header and body columns looks equal.
See example when the right panel has 1000px width:
But after resizing to 500px header width is broken again:
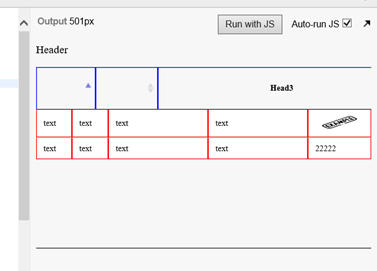
So initially size might look good but any resizing breaks it again.
2) Also, we are using custom CSS for datatables so adding official styles for datatables could be problematic as it could conflict with existing styles and makes the table looks different.
For example, the initial table has fixed width and looked like this on 1000px width:
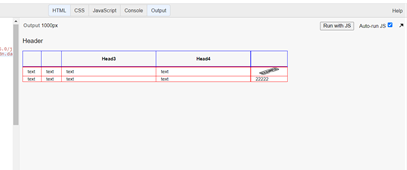
For your example it looks next:
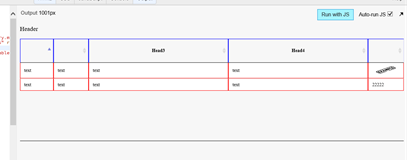
As you see fixed width doesn’t work and table looks different.
3) I also see a problem with headers when scrollX and scrollY are active simultaneously.
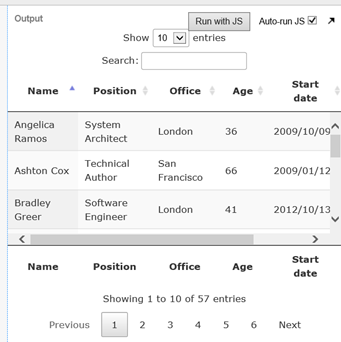
By adding them to datatables basic example the initial table looks good with 500px right panel size:
But after resizing to 1000px we will see next:
I’m not sure if this is the same issue or related. This is reproduced for Chrome too.
See live example for this:
http://live.datatables.net/wuhuvobi/1/edit
Best Regards,
Volodymyr